Intuición y matemáticas

La belleza de las matemáticas radica en ver la verdad sin esfuerzo
George Polya

El científico indio C. P. Mahalanobis (1893-1972) cuenta la siguiente anécdota. En una ocasión hizo una visita a su amigo Srinivasa Ramanujan (1887-1920) quien lo recibió justo cuando estaba preparando el desayuno. Mientras Mahalanobis esperaba que Ramanujan terminara su labor, se dio a la tarea de resolver un acertijo matemático publicado en el periódico del día. Habiendo resuelto el problema, Mahalanobis se dirigió a su amigo diciendo “he aquí un problema para ti”. Ramanujan escuchó el problema y sin dejar de preparar el desayuno, casi de inmediato comunicó su solución a Mahalanobis. Sorprendido por la rapidez de la respuesta, Mahalanobis quiso saber más sobre la solución propuesta por su amigo. Resulta que Ramanujan encontró no solamente una solución, sino un número infinito de soluciones. Cuando se le preguntó a Ramanujan cómo había resuelto el acertijo, él contestó, “cuando escuché el problema, de inmediato me di cuenta de que la solución debía ser una fracción continua. Entonces me pregunté cuál fracción continua debía ser y la respuesta apareció en mi mente en el acto. Fue así de fácil”.

Al lector no habituado a las tareas en las que el factor creatividad juegue un papel primordial, puede resultarle sorprendente el hecho de que la solución al problema haya aparecido en la mente de Ramanujan sin que al parecer fuera necesario un intenso esfuerzo mental. Desde tiempo atrás, a los matemáticos les ha interesado indagar sobre los procesos mentales que les permiten dar solución a los problemas que abordan. Vale la pena recordar la descripción que hizo Henri Poincaré de los procedimientos de los que él se valía para alcanzar la solución a las cuestiones matemáticas que a él le interesaban. Afirmó Poincaré que, por lo general, el trabajo creativo consiste en al menos tres fases. El primer paso consiste en estudiar el problema de manera consciente hasta alcanzar una comprensión completa del problema que se aborda. Esto requiere un esfuerzo mental intenso y por lo tanto genera fatiga y no puede sostenerse por largos periodos de tiempo. El segundo paso en el esquema presentado por Poincaré es el de abandonar el trabajo intenso y pasar a actividades que no guarden relación con el problema al que se quiere dar solución. Esta segunda fase puede durar, horas, días, meses e incluso años. Como tercer paso, se vuelve a abordar el problema reanudando el esfuerzo mental intenso, con el resultado de que, ahora la posibilidad de alcanzar la solución es bastante mayor que cuando se realizó el intento de solución por primera vez.

Contrariamente a lo que se pudiera pensar en primer término, la función de la segunda etapa en el esquema de Poincaré, no es, al menos no solamente, la de restaurar el vigor de la potencia intelectual antes de volver a abordar la solución del problema. Poincaré resalta el hecho de que el cerebro no se queda desentendido del problema a lo largo de las horas de relajación correspondientes a la segunda etapa. Muy al contrario, se afirma que la mente sigue ocupándose del problema, pero ahora lo hace de manera subconsciente. Todo aquel que tenga cierta familiaridad con la psicología, reconocerá el hecho de que los procesos subconscientes juegan un papel de gran importancia en la vida de las personas. Lo que tal vez sea una novedad para algunos es que los procesos subconscientes también son decisivos a la hora de emprender la solución de problemas matemáticos.

El proceso mental del cual Ramanujan se sirvió para dar con la solución del problema que su amigo le planteó se llama intuición. La intuición consiste en una representación mental, muchas veces por medio de imágenes, que es inmediata y en la que no intervienen razonamientos conscientes. Siendo la intuición un recurso de trabajo tan valioso para el matemático, vale la pena resaltar algunas de sus características más relevantes.

1) La intuición no necesariamente es una forma de conocimiento. Una intuición en particular puede ser una representación falsa de la realidad. Toca a la potencia racional del individuo decidir cuándo una intuición es verdadera y cuándo es falsa.

2) Aun cuando una intuición sea falsa, ella nos puede dar una pista para alcanzar la solución al problema que nos ocupa. Esto es así, porque gracias a una intuición falsa, el intelecto puede enfocar su atención en aspectos del problema que no había considerado hasta entonces.

3) La intuición depende del conocimiento previo que el individuo haya podido asimilar acerca del área específica en el que el problema se plantea. Así, por ejemplo, si Ramanujan era capaz de generar intuiciones que lo llevaran a la pronta solución de sus problemas, era porque él invirtió innumerables horas en el estudio de las matemáticas. Este estudio dio forma a sus procesos subconscientes de manera que sus intuiciones eran lo que se suele llamar “intuiciones educadas”.

4) Existe una marcada asimetría entre la capacidad de evaluar la potencia racional de un individuo y su capacidad para generar intuiciones. Esto se debe a que las intuiciones se presentan en la mente en forma de imágenes y estas imágenes son muy difíciles de comunicar a segundas personas. Solamente cuando estas imágenes se pueden traducir a un lenguaje comprensible de manera más universal, es cuando es posible comunicar las intuiciones, ¡pero en este caso, una intuición ya ha perdido su carácter específico y ha pasado de ser imagen mental a ser discurso racional!

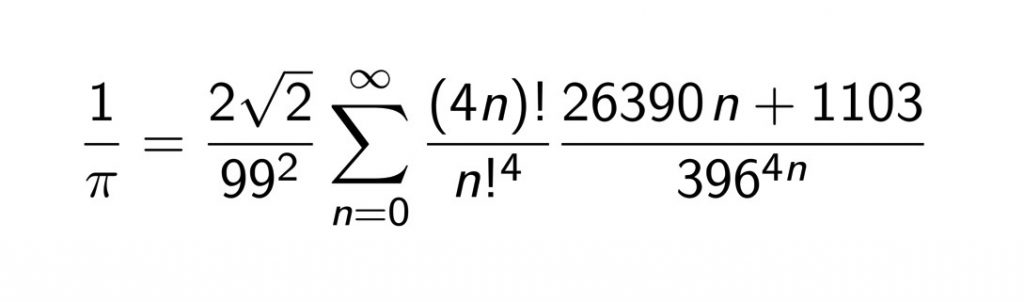
La intuición es una componente indispensable para la generación de conocimiento y puede decirse que el conocimiento más valioso proviene siempre de intuiciones generadas en capas profundas del subconsciente. Tal vez sea por esta razón que, por lo general, las teorías de mayor trascendencia encuentran oposición por parte de las comunidades a las que van dirigidas.

Una de las satisfacciones de dedicarse a las matemáticas (y seguramente a otras empresas creativas) es el atestiguar la contribución que el subconsciente aporta, a través de la intuición, a la solución de los problemas que se abordan de manera cotidiana. Esta satisfacción la comparten, tanto el investigador en su búsqueda de conocimiento nuevo, como el estudiante en sus esfuerzos de asimilar las teorías que posteriormente darán forma a las intuiciones que el subconsciente ponga a la consideración de su potencia racional. Ahora bien, si se admite que la potencia intuitiva es parte de la inteligencia humana, entonces se plantea la pregunta acerca de si la intuición puede automatizarse de modo que verdaderamente se pueda hablar de “inteligencia artificial” y esta expresión deje de parecer más bien un oxímoron. A este respecto, cabe señalar que el filósofo J. I. Friedman nos recuerda que “la intuición trabaja de manera misteriosa y no está bajo nuestro control”. Con los recursos computacionales de hoy en día, se pueden generar automáticamente muchas fórmulas que nos recuerdan las magníficas fórmulas que nos dejó Ramanujan. Sin embargo, los expertos en la obra de Ramanujan opinan que estas fórmulas carecen del encanto de las del genio indio. No son fórmulas de las que se puedan decir, ¡qué bárbaro!, ¿cómo se le pudo ocurrir algo así? Y es que las fórmulas de Ramanujan tienen un encanto que se puede comparar con la fascinación que nos produce una sinfonía de Ludwig van Beethoven. Sin embargo, para apreciar la belleza de las fórmulas de Ramanujan es necesario educar la intuición matemática.

La fórmula que aparece en la figura 2 es un buen ejemplo de los logros obtenidos gracias a la intuición de Ramanujan. Él propuso esta fórmula en 1914 pero no había certeza de su validez. En 1985, se usó la fórmula de Ramanujan para calcular 17, 526, 100 dígitos de π y una comparación con los cálculos realizados mediante otros métodos, sugería que la fórmula no podía ser falsa. Finalmente, en 1987, se logró demostrar mediante argumentos teóricos que la fórmula es correcta.