Si hoy fuera el día 365 del año, mañana no sería el día 366. Si hoy fuera el día 31 de un mes, mañana no sería el día 32. Si hoy fuera el séptimo día de la semana, mañana no sería el octavo. Entonces, hablando de días en un ciclo anual, mensual o semanal, 365 más 1 no es igual a 366, 31 más 1 no es igual a 32 y 7 más 1 no es igual a 8.
Fenómenos como estos abundan en nuestra vida diaria. Otro ejemplo típico lo encontramos en un reloj: el minutero solo marca entre 0 y 59 minutos, las horas solo van del 0 al 11. Como antes, hablando de las manecillas de un reloj resulta que 59+1 no es igual a 60 y 11+1 no es igual a 12.
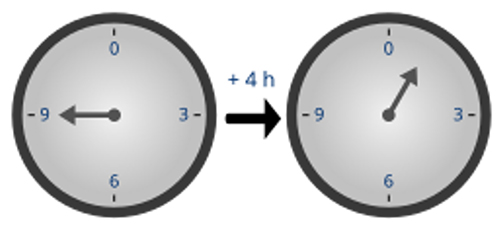
¡Pero no hay que confundirse! 365+1 sí es igual a 366 y 7+1 sí es igual a 8. Los cálculos que hicimos antes nos dan un resultado aparentemente absurdo porque se hacen dentro de un ciclo: en una semana contamos hasta 7 días y luego volvemos a empezar, en un día contamos 24 horas y volvemos a empezar. Contar así es, por lo menos, práctico. Si no juntáramos los días en años, ¡el 22 de septiembre de 2025 sería el día setecientos treinta y nueve mil quinientos diez y seis!
Analicemos más de cerca el ejemplo de los días de la semana. Supongamos que un lunes es el día 1. ¿Qué día de la semana será el día 45? Recordemos: cada siete días volvemos a empezar. Dado que 45=7+7+7+7+7+7+3, el día 45 coincide con el día 3, es decir, un miércoles. ¿Qué día de la semana es el día 57? ¿Y el 201994758629304? La lectora o el lector habrán reconocido que el algoritmo para responder estas preguntas consiste en dividir el número entre 7 y encontrar el residuo; si el residuo es 0 el día es domingo, al residuo 1 le corresponde el lunes y así sucesivamente. Calculadora en mano, podríamos adivinar a qué día de la semana corresponde cualquier número.
Cada ejemplo que discutimos previamente se explica a través del llamado algoritmo de la división. Este afirma lo siguiente: dados dos números a y b, existen otros dos números q y r que satisfacen la ecuación b=qa+r, donde r es un número entre 0 y a-1. El número q es llamado el cociente y r el residuo. Por ejemplo, si a=7 y b=45 entonces el cociente es 6 y el residuo es 3. Así, 45=6*7+3. Ahora bien, para adivinar el día de la semana en la situación del párrafo anterior usamos el algoritmo con a=7 y el número r nos indica el día que buscamos. Para los días del año aplicamos el algoritmo con a=365 y para los minutos en una hora aplicamos el algoritmo con a=60.
El algoritmo de la división es la herramienta básica para estudiar la llamada aritmética modular. En esta aritmética uno cuenta como en los ejemplos discutidos previamente: para un número dado, contamos hasta ese número y luego volvemos a empezar. Esto representa el inicio de un área de las matemáticas conocida como la teoría de números. Es muy famosa la frase, atribuida a Carl Friedrich Gauss, que dice que las matemáticas son la reina de las ciencias y la teoría de números es la reina de las matemáticas.

En sus orígenes, la teoría de números se encargaba exclusivamente de estudiar propiedades aditivas y multiplicativas de los números que usamos para contar y era considerada un área abstracta de las matemáticas. Con el paso del tiempo, la comunidad matemática y profesionales de otras disciplinas se dieron cuenta del enorme potencial que tiene esta teoría. Hoy en día la utilizamos en computación, en la protección de datos, en la criptografía, en el arte, en música y así, un largo etcétera.
Etiquetas: CCM, 2025, BUM 114, Algoritmo de la división, Carl Friedrich Gauss